Visit DIX: German-Spanish-German dictionary | diccionario Alemán-Castellano-Alemán | Spanisch-Deutsch-Spanisch Wörterbuch

next up previous contents [cite] [home]
Next: Example Images Up: Diffusion Tensor Imaging Previous: Bibliography   Contents

Subsections
Download Software


Functions Documentation

tensor.h

Functions in this class mainly provide a way to simple use tensors and apply basic mathematical operations on them. The data stored in a tensor is a floating point precision array: float _t[9]
where the indexing is

\begin{displaymath} \mathtt{ \left(\begin{array}{ccc} \_t[0] &\_t[1] &\_t[2]\\ ... ...t[4] &\_t[5]\\ \_t[6] &\_t[7] &\_t[8]\\ \end{array}\right) } \end{displaymath}

The only private function is
void eigsort(const double *W, int *i) const;
which sorts the eigenvalues by size and is used in eig(...).

Three different constructors allow the generation of an empty tensor (all values are set to zero), a symmetric tensor where the indexing corresponds to

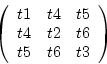
\begin{displaymath} \mathtt{ \left(\begin{array}{ccc} t1 & t4 & t5\\ t4 & t2 & t6\\ t5 & t6 & t3\\ \end{array}\right) } \end{displaymath}

and a full tensor with nine independent values.

tensor();
tensor(float t1, float t2, float t3, float t4, float t5, float t6);
tensor(float t1, float t2, float t3, float t4, float t5, float t6, float t7, float t8, float t9);

Three corresponding functions are available to set the values after the initialization:

void setZero();
void set(float t1, float t2, float t3, float t4, float t5, float t6);
void set(float t1, float t2, float t3, float t4, float t5, float t6, float t7, float t8, float t9);

float get(const int i, const int j) const;
returns the value at position $i,j$ in the tensor where $0\le i,j \le 2$ and
bool isZero() const;
checks if the tensor is empty, i.e. all values are zero and returns true if so.

The basic mathematical operations can be performed between tensors and between tensors and scalars. Dividing a scalar by a tensor is not a legal operation.

tensor operator+ (const tensor &s, const tensor &t);
tensor operator+ (const tensor &t, const float x);
tensor operator+ (const float x, const tensor &t);

tensor operator- (const tensor &s, const tensor &t);
tensor operator- (const tensor &t, const float x);
tensor operator- (const float x, const tensor &t);

tensor operator* (const tensor &s, const tensor &t);
tensor operator* (const tensor &t, const float x);
tensor operator* (const float x, const tensor &t);

tensor operator/ (const tensor &s, const tensor &t);
tensor operator/ (const tensor &t, const float x);

tensor operator- (const tensor &t);
The last functions changes the sign of a tensor.

To send a tensor to the standard output the operator
ostream &operator « (ostream &out, const tensor &t);
is used, which will print the tensor values like
Tensor values:

\begin{displaymath} \begin{array}{lll} [ \mathtt{5 } & \mathtt{ 20 } & \mathtt{... ...;}\\ \mathtt{ 25} & \mathtt{ 30 } & \mathtt{ 15 ]}\end{array}\end{displaymath}

which allows easy copy-paste into matlab.

Basic mathematical operations are: 

float det() const 		the determinant

float trace() const 		the trace (see invariant $I_1$ inequation 4.6)

tensor inv(tensor &result) const 		the inverse of a 3 $\times$3 matrix

tensor trans(tensor &result) const 		the transpose of a 3 $\times$3 matrix

To compute the eigenvalue, -vector decomposition (see equation 4.5) the CLAPACK function dsygv_(...) is called. The eigenvalues are returned so that they can be directly used to instantiate an eigensystem. The last argument must be 1 if the eigenvalues and eigenvectors should be sorted in descending order.
int eig( float &eig1, float &eig2, float &eig3, float *vector1, float *vector2, float *vector3, const int sort=0) const;

The single value decomposition also calls a CLAPACK function (see equation 7.30) whereas CLAPACK returns directly $V^T$ instead of $V$.
int svd( float &r1, float &r2, float &r3, tensor &q, tensor &s);
The equivalence between equation 7.30 and the function call is:

$\displaystyle A$ $\textstyle =$ $\displaystyle U\Sigma V^T$  
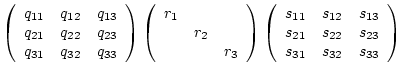  $\textstyle =$ $\displaystyle \left( \begin{array}{ccc} q_{11} & q_{12} & q_{13} \\ q_{21} & q... ... s_{21} & s_{22} & s_{23} \\ s_{31} & s_{32} & s_{33} \\ \end{array} \right)$  

so that the rotation matrix $W = UV^T$ is $qs$.

The following measurements can be computed: 


float euclid() const 		euclidian magnitude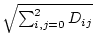$\sqrt{\sum_{i,j=0}^2 D_{ij}}$

float Max() const 		maximal value in tensor

float Min() const 		minimum value in tensor

The boolean comparison between two tensors is based on the function
float measure()const {return euclid();};
so that $\le$, $\ge$, $>$ and $<$ are defined. The comparisons $=$$=$ and $!=$ are based on every single component of the tensor.

Use of the following functions should be avoided whenever possible since they use the expensive eig(...) functions to compute the eigenvalue, -vector decomposition and only return one value. It is probably better to create an eigensystem (instance of class eigen.h) and derive this measurements from there. 


float* eigvec1(float *vector) const; 		first eigenvector, corresponding to largest eigenvalue

float* eigvec2(float *vector) const; 		second eigenvector

float* eigvec3(float *vector) const; 		third eigenvector, corresponding to smallest eigenvalue



float eigval1() const; 		first (largest) eigenvalue

float eigval2() const; 		second eigenvalue

float eigval3() const; 		third eigenvalue



float anisotropy() const; 		anisotropy, see equation 4.17

eigen.h

The data stored in a eigensystem are three floating point precision values and three floating point precision arrays, which are all private members of eigen.h:
float _lambda1, _lambda2, _lambda3;
float _vector1[3], _vector2[3], _vector3[3];
The eigenvalues are sorted so that _lambda1 is always the largest eigenvalue.

The constructors are: 

eigen(const float eig1, const float eig2, const float eig3, const float *vec1, 


const float *vec2, const float *vec3);


a constructor which initializes all values

eigen();		a constructor which sets all values to zero.
To set values in an eigensystem there are several specialized functions: 

void set(const float eig1, const float eig2, const float eig3,const float *vec1, 

const float *vec2, const float *vec3);		set all the values in an eigensystem.

void set(const float eig1, const float eig2, const floateig3);


set the eigenvalues.

void setVectors(const float *vec1, const float *vec2, constfloat *vec3);


set the eigenvectors.

void setVector2(const float x, const float y, const floatz);


sets the second eigenvector to be $\hat{\mathbf{e}}_2 = (x, y, z)^T$.

void resetVector3();		sets the third eigenvector to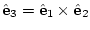$\hat{\mathbf{e}}_3 = \hat{\mathbf{e}}_1 \times \hat{\mathbf{e}}_2$

void setZero(); 		sets all the values to zero.
If the largest eigenvalue is zero then the whole eigensystem is zero. Therefore the last function only needs to set _lambda1 to zero.

The single values can be accessed with: 

float value1() const;		 largest eigenvalue 

float value2() const;		 second eigenvalue

float value3() const;		 smallest eigenvalue



float vector1(const int index) const;		  returns element ''index'' (0$\vert$1$\vert$2) of eigenvector 1

float vector2(const int index) const;		  returns element ''index'' (0$\vert$1$\vert$2) of eigenvector 2

float vector3(const int index) const;		  returns element ''index'' (0$\vert$1$\vert$2) of eigenvector 3



void print() const;		sends the eigensystem to the standard output
The operators defined are: 

bool isZero() const;		 check if eigensystem is zero (true if so)

bool operator==(const eigen &e) const;		 compares all elements of the eigensystem, no tolerance

bool operator!=(const eigen &e) const;		 do.

bool operator< (const eigen &e) const;		 less then, uses measurement specified in measure()

bool operator> (const eigen &e) const;		 do.

bool operator<=(const eigen &e) const;		 do.

bool operator>=(const eigen &e) const;		 do.
Functions are: 

void scale(const float factor); 		 scale eigensystem by ''factor''

void scale(const float x, const float y, const float z);


scale differently in each direction

void rotate(const float pitch, const float roll, const floatyaw);


Rotate eigensystem, the angles pitch, roll, and yaw


have to be provided in degrees



float det() const;		 determinant of the tensor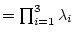 $= \prod_{i=1}^3\lambda_i$ 

float relation_Lambda1_Lambda2() const; 		 absolute value of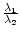 $\frac{\lambda_1}{\lambda_2}$ 

float relation_Lambda1_Lambda3() const; 		 absolute value of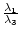 $\frac{\lambda_1}{\lambda_3}$ 



void eigen2tensor(tensor &t) const; 		 converts an eigensystem into a tensor

int tensor2eigen(const tensor &t);		 converts a tensor in an eigensystem


negative return value is an error, 1 is success




measurement of how close diffusion tensor shape is to

float close_line() const; 		 a line (equation 4.13)

float close_plane() const;		 a plane (equation 4.14)

float close_sphere() const; 		 a sphere (equation 4.15)


anisotropy measure describing deviation

float anisotropy() const; 		 from the spherical case(equation 4.17)
Functions between two eigensystems: 

float cosinMaxEigen(const eigen &e) const;


angle between the vectors of the maximum eigenvalues



bool isSimilar(const eigen &e, const float tolerance, constint similarity) const;


compare 2 eigensystem, return 1 if identical, 0 else

bool hasSimilarShape(const eigen &e, const float tolerance)const


do.

bool hasSimilarSize(const eigen &e, const float tolerance) const;


do. 

bool hasSimilarDirection(const eigen &e, const float tolerance) const;


do.

bool threshold(const float threshold=0.8) const; 


return true if eigensystem above threshold

basefield.h

Private members of the class basefield.h read the values either from the console or an xml-file: 

float readfloat(DOM_Node& node); 		read numerical valuesfrom node in xml file;


return -1 if no value present


read string from node in xml file;


return -1 if no value present

int readstring(DOM_Node& node, char* mystring);


read attribute as string from node in xml file;


return -1 if no value present


pre:mystring is the name of the attribute to get value


post: mystring is the value of the attribute;

int readattribute(DOM_Node& node, char* mystring);

void readfile(DOM_Node& node);		read the location of the datafile from node in xml file (could be removed)

void readdata(DOM_Node& node);		read the xml file and extract the data wanted;

void readmanualy(); 		read ALL values from console

void readmanualy(int& value); 		read value from console, exit if entered -1

void readmanualy(float& value); 		do.

void readmanualy(char* value);		do.

void assert_values(); 		check if all values to write xml-header are present


if not, ask for values
Protected members that are only accessible to the derived classes are: 

int _dimx, _dimy, _dimz; 		the dimensions of the field

float _deltax, _deltay, _deltaz; 		the distance betweenvoxels = voxel dimensions



char *_datafile; 		pointer to the data file

char *_orientation;		orientation of the field: axial, coronal, saggital

char *_sourcefile; 		location of source to derive tensor file

char *_originalfile; 		location of the original data




baby specific data:

int _gestationalAge;		Gestational age of the baby in weeks

int _mrNumber;		Patient ID number 

int _studyNumber;		Study number

int _seriesNumber;		Series number for the diffusion data 

char * _date;		Date of the scan
Any new element added to the DTD should be added here.

Public members, i.e. functions accessible by any program are: 

		do everything needed to call readdata, should not need

void read_XMLHeader( const char xmlFile[]);


any editing when changing DTD

void write_XMLHeader(const char xmlFile[]); 


write a xml-header file at location xmlFile




set values

void setNumbers(const int age, const int patient_id, const int studyNr, 


const int seriesNumber);

void setDate(const char* date);

void setOrig(const char* orig);

void setOrientation(const char orientation);




set the voxel dimensions for field

void setDelta(const float deltax, const float deltay, const float deltaz);


get the voxel dimensions for field

void getDelta(float& deltax, float& deltay, float& deltaz);


get the volume dimensions for field

void getDimension(int& dimx, int& dimy, int& dimz);



char * getPath(char * path); 		 get the path to the data without any extension
The actual path to the data is generated in the derived class by appending the corresponding extension.

No function to set the volume dimensions is provided, since this is either already defined by the data set and therefore in the xml-header or a new data set is created and then the corresponding derived class has to set this values.

Finally three generic functions are included in this class: 


		 check boundaries for offset and window-size


and reset them if necessary.


used for display purposes:


Plane rotates the window depending on window-size


plane[3] = 2: Image is in xy-plane

= 1: Image is in xz-plane

= 0: Image is in yz-plane


in each case plane[0] and plane[1] 


are the xy dimensions in the image coordinate system


plane[2] the number of images 

void check_boundaries(int offset[3], int windowsize[3], int plane[4]=NULL) const; 



short * read_pic(short *image,char path_file[], int offset=0);

unsigned short * read_pic(unsigned short *image, char path_file[], int offset=0);
The last two functions read the content of the *.pic files generated by LSDI_recon.

convert

The program convert is used by typing:
./convert -i=infile -o=outfile [options]
where infile and outfile are the full path and filename to the data. No file extensions are needed and the conventions described in section 5.2 are used: tensor data has the extension .ten, eigen data .eig and the background .bg. In case the type of the infile is ''raw'' then the infile is the path and the name of the files from which to derive the tensors, but without the ending XXX.pic. As output the data as well as an xml-Header is written, as long as an eigensystem is involved in the output. Table A.1 explains the options for convert.

Table A.1: Parameters for the program convert
Call Default Description
-all -it=raw convert from raw to tensor AND eigen
-it=(raw$\vert$tensor$\vert$eigen) raw type of infile
-ot=(tensor|eigen) tensor type of outfile
-ix= 256 x-dimension of infile
-iy= 256 y-dimension of infile
-iz= 1 z-dimension of infile
-ox= same as input x-dimension of outfile
-ox= same as input y-dimension of outfile
-oz= same as input z-dimension of outfile
-dx= 1 x-voxel dimension
-dy= 1 y-voxel dimension
-dz= 1 z-voxel dimension
-offx= 0 x-offset for outfile
-offy= 0 y-offset for outfile
-offz= 0 z-offset for outfile
-id= 0 Patient ID
-ex= 0 Examen number
-ser= 0 Series number
-ag= 0 Age
-or=(s$\vert$c$\vert$a) a Orientation: saggital, coronal or axial
-orig= notAvailable location of the original data
-date=   actual date (default is empty)
-r= -1 remove strips, 0 outside the object
    1 outside and inside the object


rigidreg

rigidreg is simple to use. It only takes three arguments:
./rigidreg moving-xml-file stationary-xml-file interpolation-method=(1|2)
the interpolation method can be either linear (1) or nearest neighbor (2) as described in Section 6.2.


nonrigidreg

The program nonrigidreg is used by typing:
./nonrigidreg imagetype [options] [processing-options]
where imagetype is a value vetween 0 and 4, which selects the type of input and output and is described in table A.2. All the options with their default values are shown in table A.3

Table A.2: Image type for nonrigid registration
0 synthetic image, synthetic displacement; no input needed
1 MRI input image, synthetic displacement
2 MRI input and output image
3 xml input representing tensordata, synthetic displacement
4 xml input and output representing tensordata



Table A.3: Parameters for the nonrigid registration program
Call Default Type Description
-i$=$ movingfile char array MRI or xml-file
-s$=$ stationaryfile char array MRI or xml-file
-o$=$ outputfile char array path where to save output, will be same of same type as input
-syn$=$ none char array path to synthethic displacement fields saved as floats
-x$=$ 256 integer x-dimension for MRI file
-y$=$ 256 integer y-dimension for MRI file
-z$=$ 1 integer z-dimension for MRI file
-mw$=$ 7 inpair integer size of moving window$=$window measuring correlation
-sw$=$ 7 inpair integer size of stationary window$=$window where match is searched
-sc$=$ 1 integer number of scales to match
-scf$=$ 2 integer scale factor for multiscale matching (only if sc$>$1)
-sl$=$ 0 integer gauss-filterlength before downsampling
-n$=$ 3 inpair integer neighborhood where expectance of derivatives is computed
-st$=$ 0.01 float threshold for $\sigma$ in the point-detection
-pt$=$ 0.0005 float threshold for extracted points
-k$=$ 9 integer number of neighbors for kriging interpolation
-astep$=$ 2 integer time step for anisotropic diffusion
-aiter$=$ 10 integer number of iterations in anisotropic diffusion
-acon$=$ 0.5 float contrast value for anisotropic diffusion
-anoise$=$ 0.8 float noise value for anisotropic diffusion
-g$=$ 1 3, 5, 7 Gauss-filterlength (after anisotropic diffusion,
      before pointextraction)
-d$=$ 10 integer for maximum displacement in synthetic random displacement
-r$=$ 10 integer $>=$d ratio of pixels in sparse synthetic random displacement
-grid$=$ 32 integer size of synthetic grid
-border$=$ 64 integer size of border in synthetic grid
-ran$=$ 123456 integer to initialize random numbers
-l$=$ 1 integer loop for applying matching several times


Document Type Definition

<!ELEMENT spl_tensor (header, data)>
<!ATTLIST spl_tensor version CDATA #REQUIRED> <!- the version of this DTD ->

<!- Header Section ->

<!ELEMENT header (mrNumber?, studyNumber?, seriesNumber?, age?, original?, source, file)>

<!ELEMENT mrNumber (#PCDATA)> <!- MR number ->
<!ELEMENT studyNumber (#PCDATA)> <!- study number ->
<!ELEMENT seriesNumber (#PCDATA)> <!- series number ->
<!ELEMENT age (#PCDATA)>
<!ATTLIST age type (normal | gestational) "normal"> <!- babies: gestational age ->

<!ELEMENT original (#PCDATA)> <!- path where the data was graped from ->
<!ATTLIST original date CDATA #IMPLIED> <!- when the data was graped ->
<!ATTLIST original datatype (short | float | double) "short">
<!ATTLIST original byteorder (LSB | MSB) "MSB" >
<!ATTLIST original orientation (axial | coronal | saggital) "axial">

<!ELEMENT source (#PCDATA)> <!- path where the data was loaded ->
<!ATTLIST source date CDATA #IMPLIED> <!- when the data was loaded ->
<!ATTLIST source datatype (short | float | double) "short">
<!ATTLIST source byteorder (LSB | MSB) "MSB" >
<!ATTLIST source orientation (axial | coronal | saggital) "axial">

<!ELEMENT file (#PCDATA)> <!- path where the actual file resides, no extensions ->
<!ATTLIST file date CDATA #IMPLIED> <!- when the file was first created ->
<!ATTLIST file datatype (short | float | double) "float">
<!ATTLIST file byteorder (LSB | MSB) "MSB" >
<!ATTLIST file orientation (axial | coronal | saggital) "axial">

<!- Data Section ->

<!ELEMENT data (dimensions, description?)>

<!ELEMENT description (#PCDATA)>

<!ELEMENT dimensions (volumesize, voxelsize)>
<!ELEMENT volumesize (dim_x, dim_y, dim_z)>
<!ELEMENT voxelsize (delta_x, delta_y, delta_z)>

<!ELEMENT dim_x (#PCDATA)>
<!ELEMENT dim_y (#PCDATA)>
<!ELEMENT dim_z (#PCDATA)>
<!ELEMENT delta_x (#PCDATA)>
<!ELEMENT delta_y (#PCDATA)>
<!ELEMENT delta_z (#PCDATA)>


Example xml-Header

$<$?xml version="1.0" encoding="iso-8859-1"?$>$
$<$!DOCTYPE spl_tensor SYSTEM "/home/rsierra/c++/tensor/data/spl_tensor.dtd"$>$

$<$spl_tensor version="1.0"$>$
$<$header$>$
$<$original date="11.2000" orientation="axial"$>$/d/stockholm/data/diffusion
/highresdata/axial$<$/original$>$
$<$source date="11.2000" orientation="axial"$>$/projects/shortterm/warfield
/rsierra/examples/multislice/westin/axial/tensor/axial-S$<$/source$>$
$<$file date="29.12.2000" orientation="axial"$>$/projects/shortterm/warfield
/rsierra/examples/mydata/westin$<$/file$>$
$<$/header$>$
$<$data$>$
$<$dimensions$>$
$<$volumesize$>$
$<$dim_x$>$256$<$/dim_x$>$
$<$dim_y$>$256$<$/dim_y$>$
$<$dim_z$>$24$<$/dim_z$>$
$<$/volumesize$>$
$<$voxelsize$>$
$<$delta_x$>$0.859375$<$/delta_x$>$
$<$delta_y$>$0.859375$<$/delta_y$>$
$<$delta_z$>$2.500000$<$/delta_z$>$
$<$/voxelsize$>$
$<$/dimensions$>$
$<$/data$>$
$<$/spl_tensor$>$

next up previous contents [cite] [home]
Next: Example Images Up: Diffusion Tensor Imaging Previous: Bibliography   Contents
Raimundo Sierra 2001-07-19